
The other (perhaps more rigorous) answer involves properties of complex numbers. A logarithm with base 10 is called a common logarithm, and it is expressed as log ( x ). Where $f(x) < 0$, (the case we are concerned about), $ln|f(x)| = ln(-f(x))$ and the derivative $\frac$ wouldn't be defined either.
#How to take the derivative of log how to
In the following lesson, we will look at some examples of how to apply this rule to finding different types of derivatives. The derivatives of the natural logarithm and natural exponential function are quite. One of the rules you will see come up often is the rule for the derivative of lnx. When we take the logarithm of a number, the answer is the exponent. I am trying to provide a bit more clarity for anyone who might still be confused by the comments.Īs Hans Lundmark points out in his comment, you can consider $ln|f(x)|$, which works for negative and positive values of any function $f(x)$. Part of calculus is memorizing the basic derivative rules like the product rule, the power rule, or the chain rule. This is going to be a lot easier to differentiate because we have a bunch of terms being added and subtracted instead of multiplied and divided. In other words taking the log of a product is equal to the summing the logs of each term of the product. We've done everything we can (notice that the fourth term, which has a log inside of a log, can't be further simplified). The product property of logs states that ln(xy) ln(x) + ln(y). from sympy import Symbol, Derivative import numpy as np import math x Symbol('x') function 50(math.log(5x+1)) deriv Derivative(function, x) deriv. Since ln is the natural logarithm, the usual properties of logs apply.
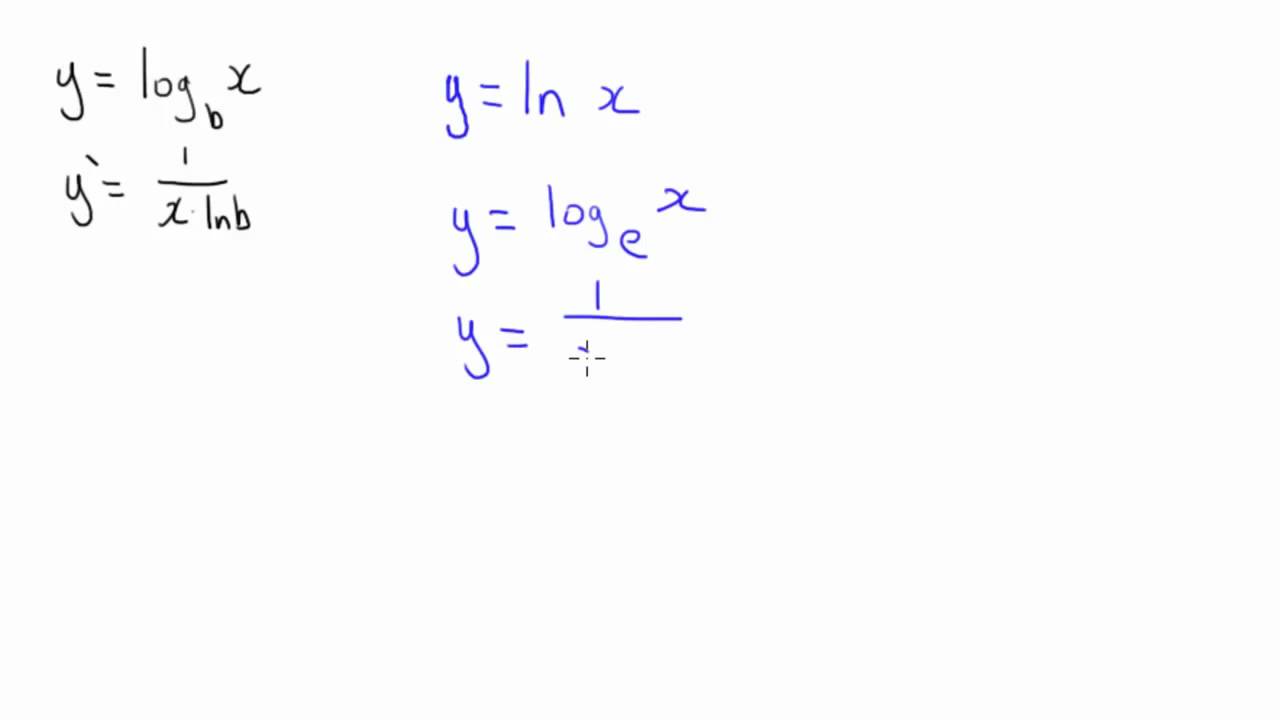
Downvoters, could you please comment on the vote? If I made a mistake or the answer is not helpful, I'd like to learn from it and improve my future answers. f ( x) log b ( x) The derivative of the logarithmic function is given by: f ' ( x) 1 / ( x ln ( b) ) x is the function argument. Finding the derivative of ln(2x) using log properties.


 0 kommentar(er)
0 kommentar(er)
